Si considerano reti senza fili in cui possono presentarsi
interferenze causate dalla trasmissione simultanea di pacchetti
da parte di due stazioni diverse, ma vicine, che usino la stessa frequenza
per comunicare.
Si è studiato il problema di assegnare
le frequenze alle stazioni base delle reti non cablate
così che siano evitate le interferenze
fra stazioni adiacenti, sia rispettata la distanza di almeno
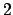 per il riuso delle frequenze, e
la soluzione utilizzi
il minor numero possibile di frequenze.
In particolare, rappresentate le frequenze con colori (per semplicità
indicati con numeri interi),
le stazioni base della rete con i vertici di un grafo,
e posto un arco fra due vertici se le stazioni sono una
nell'area di trasmissione
dell'altra, il problema si modella come
una colorazione, con il minimo numero di colori, di un grafo.
Tale problema è NP-hard per generici grafi.
Pertanto, sono state proposte soluzioni ottime
per famiglie speciali di grafi, quali anelli, alberi, reti
esagonali e reti cellulari, che ben si prestano a modellare
reti senza fili. Generalizzando, dati il grafo che modella la rete,
la distanza di riuso
per il riuso delle frequenze, e
la soluzione utilizzi
il minor numero possibile di frequenze.
In particolare, rappresentate le frequenze con colori (per semplicità
indicati con numeri interi),
le stazioni base della rete con i vertici di un grafo,
e posto un arco fra due vertici se le stazioni sono una
nell'area di trasmissione
dell'altra, il problema si modella come
una colorazione, con il minimo numero di colori, di un grafo.
Tale problema è NP-hard per generici grafi.
Pertanto, sono state proposte soluzioni ottime
per famiglie speciali di grafi, quali anelli, alberi, reti
esagonali e reti cellulari, che ben si prestano a modellare
reti senza fili. Generalizzando, dati il grafo che modella la rete,
la distanza di riuso
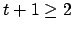 , ed un vettore di separazione
, ed un vettore di separazione
![\bgroup\color{black}$ [\delta_1, \delta_2, \ldots, \delta_{t}]$\egroup](img7.png) ,
il problema di allocare le frequenze consiste nell'assegnare
ad ogni nodo
,
il problema di allocare le frequenze consiste nell'assegnare
ad ogni nodo
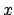 del grafo
un colore
del grafo
un colore
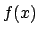 , tale che lo scarto tra
, tale che lo scarto tra
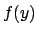 ed
ed
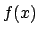 non scenda sotto
non scenda sotto
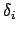 ogniqualvolta la distanza (numero minimo di archi) tra le stazioni
ogniqualvolta la distanza (numero minimo di archi) tra le stazioni
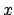 ed
ed
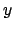 è uguale a
è uguale a
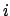 , minimizzando il massimo colore usato.
Una colorazione del grafo
che soddisfi tale vettore di separazione ed usi il minimo
numero di colori è una
, minimizzando il massimo colore usato.
Una colorazione del grafo
che soddisfi tale vettore di separazione ed usi il minimo
numero di colori è una
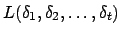 -colorazione ottima.
In [A2], per reti modellate da alberi e da grafi di intervalli,
sono presentate
-colorazione ottima.
In [A2], per reti modellate da alberi e da grafi di intervalli,
sono presentate
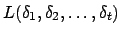 -colorazioni,
ottenute basandosi sulla nozione di vertici
'strongly-simplicial' (cioè vertici che formano
con i propri vicini, visitati in un ordine opportuno, un
grafo completo).
Gli algoritmi proposti forniscono
-colorazioni,
ottenute basandosi sulla nozione di vertici
'strongly-simplicial' (cioè vertici che formano
con i propri vicini, visitati in un ordine opportuno, un
grafo completo).
Gli algoritmi proposti forniscono
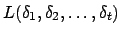 -colorazioni
-colorazioni
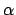 -approssimate
e richiedono tempo
polinomiale nel numero dei vertici del grafo e nella distanza di riuso.
La costante
-approssimate
e richiedono tempo
polinomiale nel numero dei vertici del grafo e nella distanza di riuso.
La costante
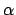 di approssimazione dipende da
di approssimazione dipende da
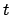 e dal vettore
di separazione.
Inoltre, per grafi di intervallo unitari,
è discusso un algoritmo che richiede tempo
lineare nel numero di intervalli
per calcolare una
e dal vettore
di separazione.
Inoltre, per grafi di intervallo unitari,
è discusso un algoritmo che richiede tempo
lineare nel numero di intervalli
per calcolare una
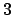 -approssimazione di
una
-approssimazione di
una
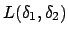 -colorazione
del grafo.
In [A7],
si presentano algoritmi efficienti per trovare
-colorazione
del grafo.
In [A7],
si presentano algoritmi efficienti per trovare
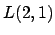 -,
-,
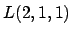 -
e
-
e
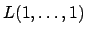 -colorazione ottime di una griglia esagonale.
Una griglia esagonale modella una rete in una regione piana, senza barriere
geografiche, dove le stazioni base sono posizionate
seguendo una tesselazione regolare del piano.
Tali griglie esagonali sono interessanti perché
richiedono meno colori per soddisfare
i vincoli di separazione di quelli richiesti da una griglia cellulare o
quadrata con lo stesso numero di vertici.
I lavori di rassegna [I3, I4]
sommarizzano e riorganizzano questi e precedenti risultati
nell'area dell'assegnamento di canali in reti non cablate.
-colorazione ottime di una griglia esagonale.
Una griglia esagonale modella una rete in una regione piana, senza barriere
geografiche, dove le stazioni base sono posizionate
seguendo una tesselazione regolare del piano.
Tali griglie esagonali sono interessanti perché
richiedono meno colori per soddisfare
i vincoli di separazione di quelli richiesti da una griglia cellulare o
quadrata con lo stesso numero di vertici.
I lavori di rassegna [I3, I4]
sommarizzano e riorganizzano questi e precedenti risultati
nell'area dell'assegnamento di canali in reti non cablate.
cristina pinotti
2007-12-19