Next: Infostations.
Up: Home
Previous: Localizzazione di utenti in reti cellulari
In [A9], è studiato il problema di allocare
risorse per la
comunicazioni (per esempio, canali di frequenze e time-slots)
alle stazioni base delle reti senza fili (WLAN, Wireless Local Loop,
reti cellulari)
in modo tale che stazioni vicine usino
frequenze molto diverse per evitare interferenze nelle trasmissioni,
le stesse frequenze siano riutilizzate solo a distanza
superiore di una soglia prestabilita e il numero di frequenze usate
sia minimo.
In particolare, sono considerate
due versioni molto realistiche del problema
di assegnamento, equivalenti a varianti di problemi
di colorazione di grafi, dove le frequenze sono rappresentate
con numeri interi.
La differenza fra le frequenze assegnate
a due stazioni adiacenti deve essere di almeno 2,
mentre la stessa frequenza può essere riutilizzata in
stazioni a distanza almeno 3 o 4.
Essendo il problema 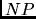 -hard, sono state proposte soluzioni ottime
per famiglie speciali di grafi, quali anelli, alberi, reti
esagonali e reti cellulari.
In questi casi particolari, la frequenza assegnabile a ciascuna stazione si
calcola in tempo costante o al piú
logaritmico.
Inoltre, in [C3],
osservato che il problema dell'interferenze
sarà sempre più esteso dato l'uso di una rete sempre più capillare,
si è generalizzato il
problema di assegnamento come segue.
Modellata la rete con un grafo, e dati la distanza di riuso
-hard, sono state proposte soluzioni ottime
per famiglie speciali di grafi, quali anelli, alberi, reti
esagonali e reti cellulari.
In questi casi particolari, la frequenza assegnabile a ciascuna stazione si
calcola in tempo costante o al piú
logaritmico.
Inoltre, in [C3],
osservato che il problema dell'interferenze
sarà sempre più esteso dato l'uso di una rete sempre più capillare,
si è generalizzato il
problema di assegnamento come segue.
Modellata la rete con un grafo, e dati la distanza di riuso 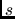 ed un vettore di separazione
ed un vettore di separazione
![$[d(1), d(2), ... , d(s-1)]$](img14.png) ,
il problema consiste nell'assegnare ad ogni nodo
,
il problema consiste nell'assegnare ad ogni nodo 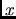 del grafo
un colore
del grafo
un colore 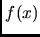 tale che lo scarto tra
tale che lo scarto tra 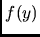 ed
ed 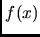 non scenda sotto
non scenda sotto
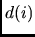 ogniqualvolta la distanza (numero minimo di archi) tra le stazioni
ogniqualvolta la distanza (numero minimo di archi) tra le stazioni 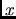 ed
ed 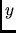 è uguale a
è uguale a 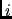 ed il massimo colore usato è minimizzato.
Per reti regolari sono
progettati algoritmi ottimi o approssimati di complessità
polinomiale sia
per distanza di riuso
ed il massimo colore usato è minimizzato.
Per reti regolari sono
progettati algoritmi ottimi o approssimati di complessità
polinomiale sia
per distanza di riuso 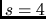 e per vettori di separazione
e per vettori di separazione ![$[1,1,1]$](img22.png) e
e ![$[2,1,1]$](img23.png) che
per distanza di riuso arbitraria
che
per distanza di riuso arbitraria 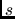 e vettori di separazione
e vettori di separazione
![$[2,1, \dots, 1]$](img24.png) .
Per le reti ad albero, a grafo di intervalli e a griglia esagonale
(Honeycomb grid),
in [C6] e in [C7], sono
stati progettati algoritmi ottimi o approssimati
di complessità polinomiale per
vettori di separazione
.
Per le reti ad albero, a grafo di intervalli e a griglia esagonale
(Honeycomb grid),
in [C6] e in [C7], sono
stati progettati algoritmi ottimi o approssimati
di complessità polinomiale per
vettori di separazione
![$[1,1,\ldots,1]$](img25.png) e
e
![$[\delta_1, \delta_2]$](img26.png) .
.
cristina pinotti
2003-10-20